Dynamic programming for sequence Alignment

According to wikipedia:
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler steps. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller^[1] and optimal substructure (described below). When applicable, the method takes far less time than naïve methods.
Top-down dynamic programming simply means storing the results of certain calculations, which are later used again since the completed calculation is a sub-problem of a larger calculation. Bottom-up dynamic programming involves formulating a complex calculation as a recursive series of simpler calculations.

In biological sequence analysis, dynamic programming is often used for sequence alignment using global sequence alignment(Needleman and Wunsch method).
Here I present a simplest interpretation of dynamic programming for aligning two sequences using global alignment(N&W method).

We have sequence 1: G A A T T C A G T T A
               sequence 2: G G A T C G A
 Here;
Length(seq1) = 11 and Length(seq2) = 7; lets call them k and l
In order to align them globally using dynamic programming method, we have to do the following;
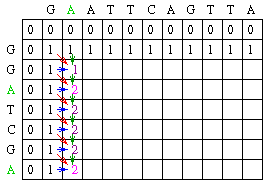
1. Build a matrix M of size (k+1) X (l+1), putting seq1 in columns and seq2 in columns
2. Initialize the matrix where M[0,0..k] and M[0..l,0] is initialized into zero[Fig -1].

 

Fig - 1

The rest of the rows and columns can be filled using the following mathematical notation:

Mi,j = MAXIMUM[
     Mi-1, j-1 + Si,j (match/mismatch in the diagonal),
     Mi,j-1 + w (gap in sequence #1),
     Mi-1,j + w (gap in sequence #2)]

where Si,j is 1 for a match and 0 for a mismatch

w = 0
 

Now, lets talk about filling M(1,1) = MAX[ {M(0,0) + S(1,1)},

                                           {M(1,0) + W},

                                           {M(0,1) + W} ] 

= MAX[ {0 + 1}, {0 + 0}, {0+0} ]

= 1

Going by this trend, M[1,2] is going to be: Max[{1+0},{0+0},{0+0} ] = 1

So, we can start filling in the matrix this way:

From this, a common observation can be drawn:

1. Increment by one the value of a cell only when there is a perfect match to 

that of the previous diagonal.

2. If there is a mismatch always continue with the value from the previous column/row.

Going by this, we can end up filling the matrix with the following values:

Now the last phase in dynamic programming:
3) Tracing back

Tracing back almost always begins with the highest score and looks to the diagonal up or to the left(gap in sequence-1) or up (gap in seq -2)

 This tracing gives an alignment:

G A A T T C A G T T A
|       |   |      |       |         |
G G A T -  C -  G  - -  A

 OR


G  - A A T T C A G T T A
|       |          |   |       |         |     
G G A  -  - T C -  G  - -  A





For longer sequences large number of other combination is possible, but the dynamic programming outputs only one result.

[Ref: Images adapted from Eric C. Rouchka's web page]

In real life examples, different penalty scores are given for a mismatch and for a gap[Every time, you go down the columns or on a row without a match should be given a penalty as a gap]